Queen's Attack II, resolvendo um exercício do HackerRank com Javascript Parte I
#0 Explicando Queen’s Attack II
Este artigo foi criado especialmente para aqueles que estão estudando Javascript.
Link para ele no HackerRank.

Imagine-se diante de um tabuleiro de xadrez, onde é fornecida a posição da rainha e um determinado número de obstáculos. Sua missão é calcular quantas casas a rainha pode atacar.
Regras:
- A rainha estará posicionada em um tabuleiro de tamanho (n x n) numerado de 1 a n, com a numeração iniciando na parte inferior esquerda, conforme ilustrado na imagem a seguir.
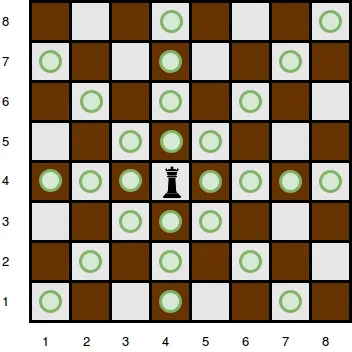
-
Cada quadrado do tabuleiro é identificado por uma tupla (r, c), onde “r” representa a linha e “c” representa a coluna.
-
A rainha está localizada na posição (r_q, c_q).
-
A variável “k” determina o número de obstáculos no tabuleiro.
-
O array “obstacles” armazena as posições dos obstáculos no tabuleiro, se houver.
-
As posições dos obstáculos são definidas como tuplas [[r, c]…].
-
É possível que vários obstáculos ocupem a mesma posição, mas nunca a posição da rainha.
-
Os obstáculos interrompem o alcance de ataque da rainha, ou seja, se um obstáculo estiver no alcance de ataque da rainha, a contagem de casas atacáveis pela rainha naquela direção será interrompida até esse obstáculo.

Dito isso, calcule o numero total de casas que a rainha pode atacar.
Função a ser completada caso queira testar seu próprio código.
function queensAttack(n, k, r_q, c_q, obstacles){
'escreva seu código aqui'
}
console.log(queensAttack(5,2,1,1, [[1,2],[5,2]]))
Para recordar, as variáveis são as seguintes:
- “n” é o tamanho quadrático do tabuleiro. Por exemplo, se “n” for 5, o tabuleiro será 5x5.
- “k” é o número de obstáculos no tabuleiro
- “r_q” é a linha em que a rainha está posicionada.
- “c_q” é a coluna em que a rainha está posicionada.
- “obstacles” é um array com tuplas que representam as posições dos obstáculos no tabuleiro. Por exemplo, [[1,2],[5,2]].
#1 Tipos de soluções

Neste artigo, apresentarei três soluções para um problema específico, cada uma delas com um nível de dificuldade diferente. A primeira solução, que eu chamaria de “nível básico”, é uma criação minha e, embora funcione, não é muito elegante. Além disso, ela peca em termos de eficiência e escalabilidade, não conseguindo atender completamente às necessidades do HackerRank.
A segunda solução é uma refatoração, buscando melhorar a legibilidade do código. Nesta solução, manteremos a lógica por trás da primeira e organizaremos o código de maneira a ocupar menos espaço. Poderíamos chamá-la de “nível intermediário”.
Por fim, a terceira solução, que chamarei de “nível avançado”, consegue atender completamente às necessidades do problema, possui uma lógica totalmente diferente das anteriores com uma alta capacidade de escalabilidade. Embora eu não possa afirmar com precisão se ela é a melhor em termos de desempenho, é certamente melhor do que as soluções anteriores. Tentarei explicar da melhor forma possivel cada uma das soluções passo a passo adiante.
#2 Minha solução
Minha solução começa com a recriação do tabuleiro em uma matriz. Isso vai causar problemas futuros, mas explicarei melhor esses problemas quando chegarmos lá. A primeira tarefa é criar uma matriz quadrada com “n” colunas e linhas, utilizei um loop “for” para tal.
function queensAttack(n, k, r_q, c_q, obstacles){
let matrix = [];
for (let i = 0; i < n; i++) {
matrix[i] = [];
for (let j = 0; j < n; j++) {
matrix[i][j] = 0;
}
}
return (matrix)
}
console.log(queensAttack(5,2,1,1, [[1,2],[5,2]]))
Você pode copiar e rodar esse código, ele ira reproduzir uma matriz de tamanho 5x5 preenchida de zeros.
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ]
]
Com isso em mente, já temos o nosso tabuleiro de xadrez pronto, o próximo passo agora é certificar de que a rainha vá para a casa correta.
Para calcular a posição da rainha no tabuleiro, criei duas constantes. Porém, é importante lembrar que o posicionamento do tabuleiro é dado como na imagem abaixo.
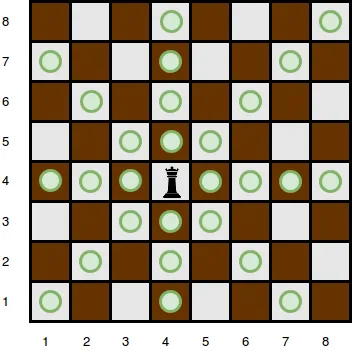
Ao contrário do tabuleiro de xadrez, onde as casas são numeradas de cima para baixo e da esquerda para a direita, as casas em uma matriz são numeradas da esquerda para a direita e de cima para baixo, começando com o índice 0. Por exemplo, se a rainha estiver na casa (4,4) no tabuleiro de xadrez, na matriz ela estaria na posição [4][3]. Para adaptar a posição da rainha para a matriz eu declarei as seguintes constantes.
const queenLinhaArray= n-r_q;
const queenColunaArray= c_q-1;
Assim eu calculo a posição utilizando a fórmula [n-(r_q)] e [(c_q)-1]. Em primeiro lugar, subtraio o tamanho do tabuleiro “n” da linha da rainha (r_q) para determinar sua posição na matriz. Em seguida, subtraio 1 da coluna da rainha (c_q) para determinar sua posição na matriz. Como exemplo, se a rainha estiver na casa 4 linha e 4 coluna no tabuleiro, na nossa matriz de tamanho 8, ela estaria na casa [4][3] como na imagem mostrada anterior.
Agora que possuímos a posição da rainha assegurada, vamos inserir ela no tabuleiro com a seguinte linha de código:
[matrix[queenLinhaArray][queenColunaArray]] = ['Q'];
Essa linha ira inserir a letra Q na posição onde foi indicada para a rainha estar, se você fez tudo certo até agora, seu resultado deve ser algo parecido com isto, uma matriz cheio de zeros e uma letra Q representando a rainha.
[
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 'Q', 0, 0, 0, 0 ]
]
Caso tenha se perdido, compare com seu código até esse ponto:
function queensAttack(n, k, r_q, c_q, obstacles){
const queenLinhaArray = n-r_q;
const queenColunaArray= c_q-1;
let matrix = [];
for (let i = 0; i < n; i++) {
matrix[i] = [];
for (let j = 0; j < n; j++) {
matrix[i][j] = 0;
}
}
[matrix[queenLinhaArray][queenColunaArray]] = ['Q'];
return (matrix)
}
console.log(queensAttack(5,2,1,1, [[1,2],[5,2]]))
Agora que temos o tabuleiro e a rainha posicionada, o próximo passo é adicionar os obstáculos. Para isso, precisamos prestar atenção na forma como eles são enviados na chamada da função. Como estamos simulando a chamada do HackerRank, vamos continuar com o modelo de entrada de um array de tuplas, como [[1,2],[5,2]]. Esse array pode conter até (nxn-1) tuplas, pois isso preencheria todo o tabuleiro com obstáculos e ainda teríamos a posição da rainha assegurada.
Para adicionar os obstáculos no tabuleiro, utilizamos um loop para iterar sobre cada tupla no array de obstáculos. Seguindo a mesma ideia do posicionamento da rainha na matriz, dentro do loop. Então, adicionamos o caractere “X” na posição calculada para representar o obstáculo no tabuleiro. Isso garante que os obstáculos sejam posicionados corretamente no tabuleiro e a cada iteração, removo uma tupla do array “obstacles”.
Passo a passo do funcionamento:
- Pego a posição da linha do obstáculo no tabuleiro subtraindo o tamanho do tabuleiro (n) com o valor da tupla linha (obstacles[0][0]).
- Pego a posição da coluna do obstáculo no tabuleiro (obstacleCol) subtraindo 1 do valor da tupla coluna (obstacles[0][1]).
- Substituo o valor na matriz na posição encontrada com ‘X’.
- Removo a tupla usada para achar a posição do obstáculo.
- Continuo o loop até que não haja mais tuplas.
Eis o código utilizado:
for (let i =0; i<k; i++){
let obstacleRow = n-(obstacles[0][0]);
let obstacleCol = (obstacles[0][1])-1;
[matrix[obstacleRow][obstacleCol]] = ['X']
obstacles.shift();
}
Pronto, com isso já somos capazes de reproduzirmos o nosso tabuleiro de tamanho n com as peças da rainha e obstáculos, se você fez tudo corretamente seu resultado atual deve ser algo assim:
[
[ 0, 'X', 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0 ],
[ 'Q', 'X', 0, 0, 0 ]
]
Agora que o tabuleiro e as peças estão devidamente posicionadas, chegamos à etapa final de nosso código. Nela, devemos encontrar uma forma de contar as casas que a rainha pode se movimentar, considerando os obstáculos no tabuleiro, uma rainha pode se movimentar em 8 direções diferentes, podemos calcular o número de casas alcançáveis em cada direção e somando estes obter o resultado.
Então é só criar um acumulador e sair acumulando as casas com loops em todas as direções, eis o código utilizado que utilizei para somar o número de casas acima na direção acima da rainha.
for (let rowUp = queenLinhaArray-1; rowUp>=0; rowUp--) {
if (matrix[rowUp][queenColunaArray] == 'X') {
break;
}
else {maxMovs+=1}
}
Para chegar à contagem final de casas que a rainha pode andar, precisamos considerar as 8 direções possíveis. Eu utilizei um loop para percorrer cada direção, verificando se a casa atual é uma posição válida (não é um obstáculo ou está fora do tabuleiro) e, caso seja, incrementando a contagem final. É importante lembrar que, durante essa verificação, devemos seguir as regras da nossa matriz em relação ao tabuleiro de xadrez, para que a contagem seja precisa.
Meu código final dessa primeira parte:
function queensAttack(n, k, r_q, c_q, obstacles){
const queenLinhaArray = n-r_q;
const queenColunaArray= c_q-1;
let matrix = [];
let maxMovs = 0;
for (let i = 0; i < n; i++) {
matrix[i] = [];
for (let j = 0; j < n; j++) {
matrix[i][j] = 0;
}
}
for (let i =0; i<k; i++){
let obstacleRow = n-(obstacles[0][0]);
let obstacleCol = (obstacles[0][1])-1;
[matrix[obstacleRow][obstacleCol]] = ['X']
obstacles.shift();
}
for (let rowUp = queenLinhaArray-1; rowUp>=0; rowUp--) {
if (matrix[rowUp][queenColunaArray] == 'X') {
break;
}
else {maxMovs+=1}
}
for (let rowDown = queenLinhaArray+1; rowDown<n; rowDown++){
if (matrix[rowDown][queenColunaArray] == 'X') {
break;
}
else {maxMovs+=1};
}
for (let turnLeft = queenColunaArray-1; turnLeft>=0; turnLeft--) {
if (matrix[queenLinhaArray][turnLeft]== 'X'){
break;
}
else {maxMovs+=1}
}
for (let turnRight = queenColunaArray+1; turnRight<n; turnRight++) {
if (matrix[queenLinhaArray][turnRight]== 'X'){
break;
}
else {maxMovs+=1}
}
for (let diagUpLeftRow = queenLinhaArray-1, diagUpLeftCol = queenColunaArray-1;
diagUpLeftRow>=0 && diagUpLeftCol>=0; diagUpLeftRow--, diagUpLeftCol--) {
if (matrix[diagUpLeftRow][diagUpLeftCol] == 'X'){
break;
}
else {maxMovs+=1}
}
for (let diagDownRightRow = queenLinhaArray+1, diagDownRightCol = queenColunaArray+1;
diagDownRightRow<n && diagDownRightCol<n; diagDownRightRow++, diagDownRightCol++) {
if (matrix[diagDownRightRow][diagDownRightCol] == 'X'){
break;
}
else {maxMovs+=1}
}
for (let diagUpRightRow = queenLinhaArray-1, diagUpRightCol = queenColunaArray+1;
diagUpRightRow>=0 && diagUpRightCol<n; diagUpRightRow--, diagUpRightCol++) {
if (matrix[diagUpRightRow][diagUpRightCol] == 'X') {
break;
}
else {maxMovs+=1}
}
for (let diagDownLeftRow = queenLinhaArray+1, diagDownLeftCol = queenColunaArray-1;
diagDownLeftRow<n && diagDownLeftCol>=0; diagDownLeftRow++, diagDownLeftCol--) {
if (matrix[diagDownLeftRow][diagDownLeftCol] == 'X') {
break;
}
else {maxMovs+=1}
}
[matrix[queenLinhaArray][queenColunaArray]] = ['Q'];
return (matrix)
}
console.log(queensAttack(5,2,1,1, [[1,2],[5,2]]))
Parabéns, terminamos o desafio!!! Ou quase…