Buscas utilizando IA · PedroVSD

Recentemente aqui no blog, um usuário chamado Zaqueu (https://www.tabnews.com.br/Zaqueu), fez um post sobre autômatos celulares e árvores na prática, assunto esse lembra bastante busca inteligentes na área de inteligência artificial, que por coincidência estou estudando esse tema na disciplina de IA na faculdade, e recentemente tive que realizar algumas implementações e alguns algoritmos, claro como é um assunto novo, tive que buscar alguma ajuda e ajustes em certa parte do código. A questão desses códigos é resolver o 8 puzzle.

Tendo dito isto, e com um questionamento do Zaqueu, “Por quê não compartilha aqui no blog também?”, resolvi fazer tal ação.

Portanto vou compartilhar com vocês meu trabalho, podem apontar pontos a serem melhorados etc, serão bem-vindos esses apontamentos. Dito tudo isso, vamos ao código. Todos os códigos estão no meu repositório do github.

https://github.com/PedroVSD/IA

Temos as seguintes implementações em árvores, BFS, DFS, IDS, busca gulosa e A*.

BFS:
Busca em largura por padrão, percorre o nós da árvore como uma “frente de onda”, passando por todos os nós na mesma altura.

DFS:
Busca em profundidade, percorre os nós até o nó mais profundo de um atual ramo, e depois sobe, até percorrer toda a árvore por inteira. Um adendo aqui, geralmente até onde sei, é mais comum se utilizar a DFS com forma recursiva, porém utilizei usando pilha para evitar loops infinitos e também um uso exorbitante de memória.

IDS:
Uma busca interativa, que visa juntar as melhores partes da BFS e DFS. Até onde entendi, funciona da segunda forma. Temos um limite de expansão dos níveis da árvore(Como na BFS), e o algoritmo realiza a DFS restringida por esse limite, e caso não encontre o caminho, esse limite é iterado em mais um, e novamente a DFS é feita.

Agora vamos falar e algoritmos um pouco mais inteligentes, a busca gulosa e o A*, que utilizam de heurísticas para encontrar um caminho.

Utilizei a heurística de Manhatam, que se baseia na distância de pontos da seguinte forma:
$DM = |x2-x1| + |y2-y1|$

Digamos que estamos no ponto azul (1,1) e queremos chegar no ponto (3,4), aplicando à distância de Manhatam temos,
$DM = |1-3| + |1-4|$ logo, Dm = 5.

Levamos em consideração as “esquinas” e não simplesmente uma reta e um ponto A até um ponto B, como na distância Euclidiana, que é basicamente um Pitágoras aplicado ao plano cartesiano $DM = sqrt((x2-x1)^² + (y2-y1)^²)$ .

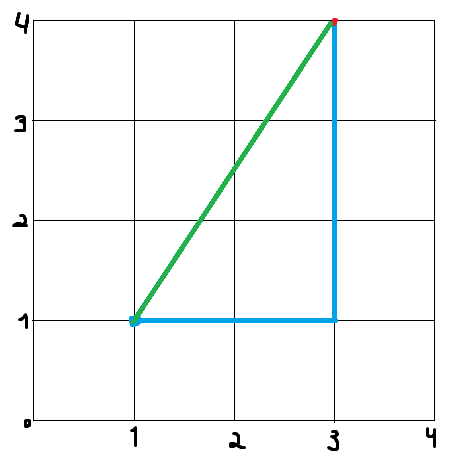
Imagem do plano cartesiano para demonstrar a heurística de Manhatam e Euclides

Em Azul temos Manhatam

Em verde temos Euclidiana

Busca Gulosa:
Na busca gulosa, como o próprio nome já diz é um algoritmo guloso, ou seja ele vai tentar todas as opções possíveis até chegar ao seu objetivo. Ele encontra o objetivo, mas não de forma ótima. Um ponto aqui, é que a busca gulosa, utiliza apenas a heurística para se guiar. Você pode pensar que o caminho é dado por uma função e essa função é a heurística. F(n) = H(n).

A* ou A estrela:
De todos, o mais inteligente, se utiliza tanto da heurística e os pesos das arestas da árvore. A função dada pelo A* é a seguinte F(n) = H(n) + G(n), em que g(n) = peso das arestas e H(n) a heurística. Podemos pensar que o A* consegue “olhar” para o passado antes de dar o próximo passo, você pode pensar como um tipo de back tracking, (técnica que o algoritmo dá um passo para trás antes e dar o próximo passo).

Creio que o principal os trabalhos foi escrito acima, claro temos funções auxiliares que tentarei descrever mais a frente.

Utilizei o seguinte estado final do tabuleiro:

objetivo_final = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 0]
]

Vou listar apenas um exemplo utilizado, devido ao limite de caracteres do post e como também é a saída do programa.

Exemplo:

tabuleiro = [
[8, 7, 6],
[5, 4, 3],
[2, 1, 0]
]

Ou seja, os algoritmos buscam sair do estado inicial até o tabuleiro final.

A seguir vou colocar as seguintes saídas dos algoritmos.

=== Solução por BFS ===

Caminho da solução: cima -> esquerda -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> esquerda -> cima -> esquerda -> baixo -> direita -> baixo -> direita

Custo da solução: 30
Nós expandidos: 181393
Tamanho da fronteira: 150
Tamanho máximo da fronteira: 24054
Profundidade da busca: 31
Profundidade máxima da busca: 31
Tempo de execução: 4.328634 segundos
Uso de memória: 196.95 MB

=== Solução por DFS (com pilha iterativa) ===

Caminho da solução: cima -> cima -> esquerda -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> direita -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> direita -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> esquerda -> esquerda -> baixo -> direita -> direita -> cima -> cima -> esquerda -> esquerda -> baixo -> direita -> direita -> baixo

Custo da solução: 100
Nós expandidos: 6979
Profundidade máxima da busca: 100
Tempo de execução: 0.029800 segundos
Uso de memória: 188.61 MB

=== Solução por IDS (Busca Iterativa em Profundidade) ===

Custo da solução: 30
Profundidade da solução: 33
Tempo de execução: 2.203781 segundos
Uso de memória: 171.76 MB

=== Solução por BFS Gulosa ===

Caminho da solução: esquerda -> esquerda -> cima -> direita -> cima -> esquerda -> baixo -> direita -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> direita -> cima -> cima -> esquerda -> esquerda -> baixo -> direita -> cima -> direita -> baixo -> baixo -> esquerda -> cima -> esquerda -> cima -> direita -> direita -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> esquerda -> baixo -> direita -> cima -> cima -> esquerda -> baixo -> direita -> baixo -> esquerda -> esquerda -> cima -> direita -> cima -> esquerda -> baixo -> baixo -> direita -> direita
Custo da solução: 58
Nós expandidos: 139
Tamanho da fronteira: 104
Tamanho máximo da fronteira: 105
Profundidade da busca: 58
Profundidade máxima da busca: 59
Tempo de execução: 0.003452 segundos
Uso de memória: 100.09 MB

=== Solução por A* ===

Caminho da solução: esquerda -> cima -> direita -> baixo -> esquerda -> esquerda -> cima -> cima -> direita -> baixo -> direita -> cima -> esquerda -> baixo -> baixo -> esquerda -> cima -> cima -> direita -> baixo -> baixo -> direita -> cima -> esquerda -> baixo -> esquerda -> cima -> direita -> direita -> baixo

Custo da solução: 30
Nós expandidos: 18030
Tamanho da fronteira: 8235
Tamanho máximo da fronteira: 8253
Profundidade da busca: 30
Profundidade máxima da busca: 30
Tempo de execução: 1.287767 segundos
Uso de memória: 120.20 MB

Podemos ver que, o melhor é o A*, pelos motivos que já comentei antes.

No código também temos funções auxiliares como já tinha dito, sendo elas
chegou_obejtivo, verifica se o tabuleiro é igual ao determinado como objetivo final.
encontrar_zero, encontra o zero no tabuleiro para que os movimentos possam ser feitos.

Expandir, expande os atuais filhos de um determinado nó.

Um ponto que gostaria de ressaltar é que a busca gulosa e o A* foram feitos aptando a BFS, creio que não é a melhor abordagem. Creio também que consegui dizer o que queria, como disse também no início do post, toda e qualquer ajuda, detalhe, conselho serão bem vindos, espero que gostem do post.

Muito obrigado se acompanhou até aqui.