Entendendo a Pesquisa Binária

Ao estudar mais a fundo sobre algoritmos e, consequentemente, lendo o livro Entendendo Algoritmos, tenho adquirido muito conhecimento e decidi compartilhar com o maior número de pessoas possível.

Hoje quero falar um pouco sobre a pesquisa binária. Para quem ainda não conhece esse conceito, vamos imaginar um problema simples: suponha que você precise localizar um registro em uma lista ordenada e o item que está procurando começa com a letra K (não que eu esteja me referindo ao meu próprio nome).

Você pode começar a busca pela primeira página e seguir uma a uma até encontrar os registros com a letra K. Mas, sendo mais estratégico, poderia pular diretamente para o meio da lista — afinal, numa lista ordenada, a letra K está próxima do meio. Isso reduziria significativamente o tempo necessário para encontrar o item.

Agora pense em outro cenário: você vai fazer login em uma rede social. O sistema precisa localizar seu usuário no banco de dados. Digamos que seu nome comece com a letra Z. Seria ineficiente iniciar a busca pela letra A, certo? Faz mais sentido começar do final ou do meio da lista.

Esses são exemplos clássicos de problemas de busca, e para otimizar essas situações utilizamos a pesquisa binária.

O que é Pesquisa Binária?

A pesquisa binária é um algoritmo de busca eficiente, que requer como entrada uma lista ordenada. Ela retorna a posição do item buscado, caso ele exista na lista. Caso contrário, retorna None.

Um Exemplo Prático

Imagine que estou pensando em um número entre 1 e 100 e desafio você a adivinhar qual é. Tente agora mesmo fazer um chute!

Antes de revelar, pense que o objetivo é adivinhar o número com o menor número de tentativas possível. Agora, imagine que você começa assim: 1, 2, 3, 4... Veja o que acontece:

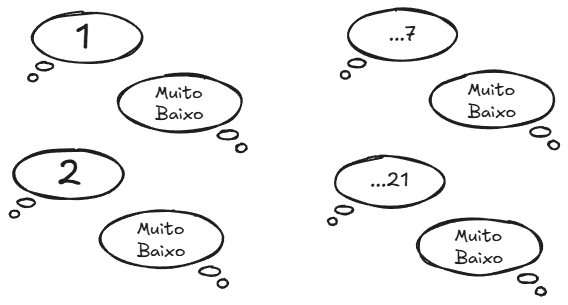
Essa abordagem se chama pesquisa simples. Embora funcione, pode levar até 100 tentativas no pior caso — o que não é nada eficiente.

Agora veja uma forma mais inteligente e assertiva de realizar essa busca:

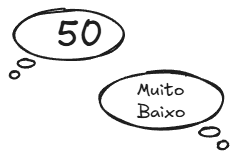
Mesmo com a resposta sendo "muito baixo", você eliminou 50 números de uma só vez, apenas por ter começado pela metade da lista (número 50).

Na próxima tentativa, você escolhe a metade do intervalo restante: 75.

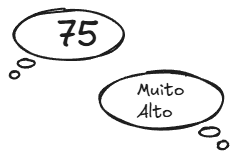
A resposta agora é "muito alto". Mais uma vez, você eliminou metade dos números restantes.

Na sequência, você tenta 63 (meio entre 51 e 74)... ainda é alto. Depois tenta 57... e acerta o número!

O Poder da Pesquisa Binária

Parabéns! Você acabou de aprender como funciona a pesquisa binária. Percebe como ela não é nenhum bicho de sete cabeças?

Enquanto a pesquisa simples poderia levar até 57 tentativas para encontrar o número 57, com a pesquisa binária conseguimos isso em apenas 4 tentativas.

Veja a comparação:

VS

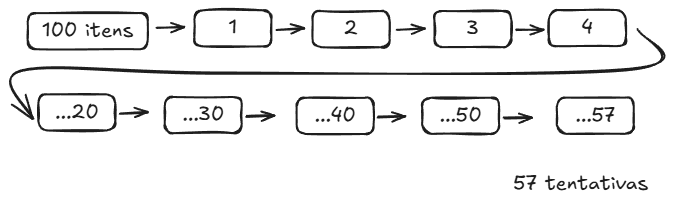
A diferença é gritante.

Pode parecer inacreditável que alguém escolha a abordagem simples, mas acredite: já fiz essa brincadeira com amigos e familiares, e a maioria começou do 1 e foi subindo.

Considerações Finais

A pesquisa binária não é uma solução mágica para todos os problemas de busca. Como vimos, ela exige uma lista ordenada para funcionar corretamente — e nem sempre isso é possível no mundo real, especialmente ao lidar com sistemas complexos ou dados não estruturados.

Ainda assim, em muitos cenários onde a velocidade de resposta é essencial, algoritmos de pesquisa binária podem ser salvadores de desempenho.